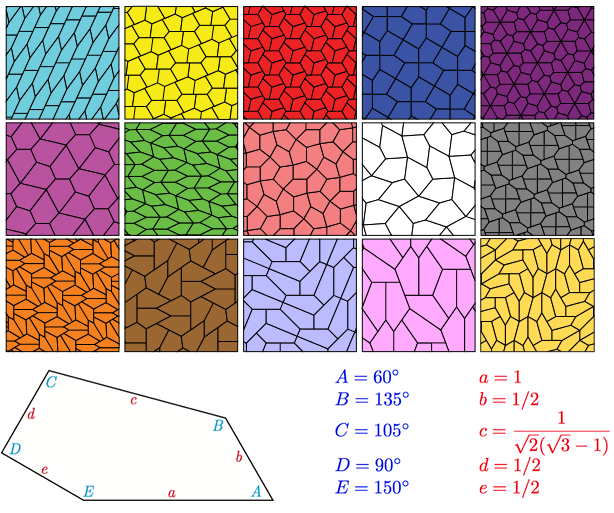
ze kterého lze složit jednolitou rovinou plochu bez mezer ze shodných stejně velkých tvarů, odhalili matematici Casey Mann, Jennifer McLoud a David Von Derau z University of Washington. Spolu se čtrnácti předchozími, které byly odhaleny dříve, si je můžeme prohlédnout v horní části obrázku (via Wikimedia Commons). Poslední objevený je vpravo dole. Jeho parametry shrnuje spodní část obrázku (obr. Casey Mann). U trojúhelníků, čtverců a šestiúhelníků jde o triviální záležitost. Vyplnit s nimi rovinu homogenně bez mezer není problém. S pětiúhelníky je to podstatně složitější. S pravidelnými pětiúhelníky to nejde vůbec. Prvních pět použitelných typů nepravidelných pětiúhelníků nalezl až roku 1918 německý matematik Karl August Reinhardt. Současný počet typů možná není konečný. Se sedmi a osmiúhelníky je to neproveditelné, což se již podařilo dokázat. Vše, co tu bylo zmíněno, platí pro konvexní mnohoúhelníky stejné velikosti a tvaru, u nekonvexních je to podstatně snazší.

S vlastnostmi pětiúhelníka souvisí i problematika pětičetné symetrie krystalů, viz akademon.cz 5.10.2011: Nobelova cena za chemii pro rok 2011.